Análisis de ruido de configuraciones de amplificador operacional: uso de técnicas de desplazamiento de fuentes

En este artículo aplicaremos los teoremas de desplazamiento de fuentes de voltaje y corriente explicados en este otro artículo.

Trabajaremos en varias configuraciones de amplificadores operacionales para obtener su expresión completa de ruido referido a la entrada. Cada fuente de ruido en la configuración del amplificador operacional será desplazada a la entrada utilizando los teoremas de desplazamiento paso a paso.

Amplificador de Voltaje No Inversor con Op-Amp – Análisis de Ruido

La figura muestra una topología típica de amplificador de voltaje no inversor con Op-Amp.

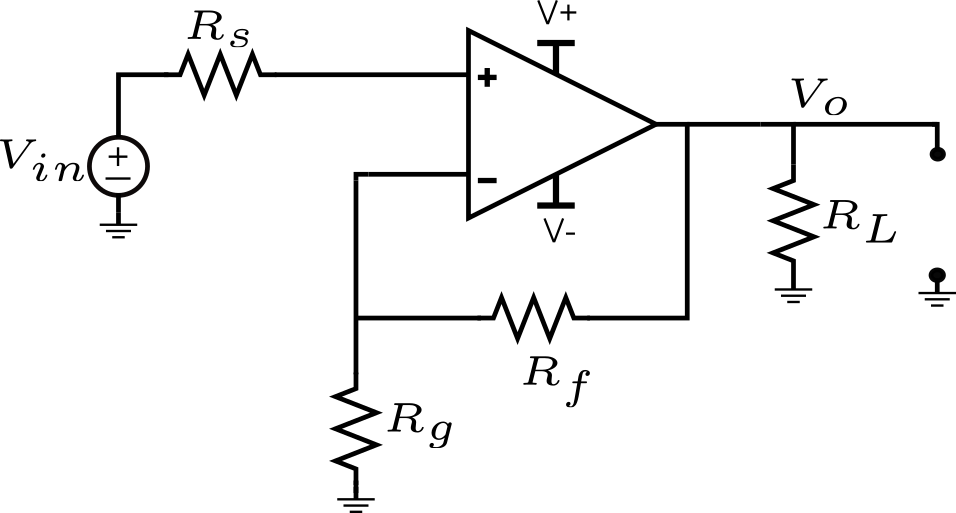
Y en la siguiente figura se muestra la misma topología de circuito con las fuentes de ruido asociadas a cada componente.

En cada subsección siguiente discutiremos cómo referir cada fuente de ruido a la entrada, de modo que podamos calcular el ruido total referido a la entrada del circuito. Una ventaja de este enfoque, en comparación, por ejemplo, con este artículo de TI es que puedes obtener la contribución de cada fuente de ruido directamente en la entrada, sin hacer las tediosas matemáticas de dividir cada término de ruido de salida por la ganancia del amplificador.

En el siguiente análisis, asumiremos el factor de ganancia \(A=\frac{R_f}{R_g + R_f}\), la ganancia bien conocida de un amplificador de voltaje no inversor con Op-Amp.

\(R_s\) – Resistencia de fuente.

La resistencia de fuente tiene una densidad espectral de potencia de ruido (PSD) asociada con ella dada por \(V_{n,R_s}^2=4kTR_s\). Dado que está ubicada en la entrada, ya está referida a la entrada. Fácil.

\(V_{n,R_L}\) – Ruido de Voltaje de la Carga

Asumiendo que tenemos una carga resistiva, está destinada a tener un PSD de ruido dado por \(V_{n,R_L}^2=4kTR_L\). TL;DR: no contribuye con ruido cuando asumimos un Op-Amp ideal.

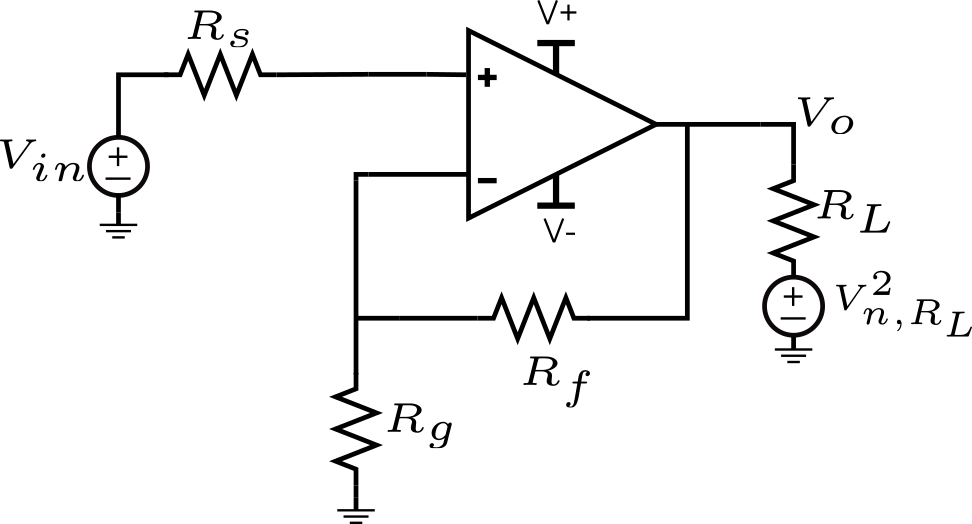
Un razonamiento y conclusión incorrectos podrían ser que esta fuente de ruido simplemente se refiere de nuevo a la entrada por el cuadrado de la ganancia del amplificador, es decir, \(\frac{V_{n,R_L}^2}{A^2}\), donde \(A=\frac{R_g}{R_g+R_f}\).

Esto es incorrecto porque \(V_{n,R_L}^2\) pasa por una transformación antes de llegar al nodo de salida de voltaje \(V_{o}\). A saber, la división de voltaje con respecto a la impedancia de salida del Op-Amp.

Si modelamos, la impedancia de salida del amplificador como \(Z_o\) en serie con su fuente controlada \(V_c\). Si usamos la superposición, podemos escribir la siguiente expresión para el nodo de voltaje de salida.

\(V_o=V_{n,R_L}\frac{Z_o}{Z_o+R_L} + V_c\frac{R_L}{Z_o+R_L}\)

Dado que hemos asumido que el Op-Amp es ideal, entonces \(Z_o=0\). Por lo tanto, \(V_{n,R_L}\) no contribuye con ruido al nodo de salida del amplificador; no es necesario referirlo de nuevo a la entrada.

No obstante, pueden surgir otras preguntas, como:

• Sabemos que \(Z_o\approx 0\) en CC en un amplificador de realimentación real, pero este valor aumenta a medida que la ganancia de lazo disminuye en altas frecuencias (para una configuración de realimentación en paralelo en la salida, como lo hace el amplificador de voltaje no inversor), ¿significa eso que en altas frecuencias la carga puede contribuir con ruido? La respuesta es sí, podríamos llamarlo ruido fuera de banda.

Para concluir, bajo la suposición de un op-amp ideal (ganancia infinita en todas las frecuencias, por lo tanto, impedancia de salida de 0), la resistencia de carga \(R_L\) no contribuye con ruido a la entrada.

\(V_{n,OA}\) – Ruido de Voltaje de Entrada del Op-Amp.

Esta fuente de ruido está directamente en serie con la fuente de entrada (igual que \(R_s\)); por lo tanto, es fácil ver que ya está referida a la entrada. Simplemente se suma al ruido que produce la fuente de entrada \(R_s\).

\(V_{n,R_g}\) – Ruido de Voltaje asociado con la resistencia de realimentación \(R_g\)

Esta fuente de ruido, como se muestra en la figura 6, puede ser referida a la entrada de muchas maneras.

• Manera común: reconocer que \(V_{n,R_g}^2\) puede ser desplazado a \(V_o\) a través de la transferencia \(\left(-\frac{R_f}{R_g}\right)^2\) y luego ser referido de nuevo a la entrada a través de la transferencia no inversora \(\left(\frac{R_g}{R_f+R_g}\right)^2\). Multiplicando cada factor obtenemos: \(V_{n,R_g}^2\left(-\frac{R_f}{R_g}\right)^2\left(\frac{R_g}{R_f+R_g}\right)^2\). Simplificando, podemos llegar a \(V_{n,R_g}^2\left(\frac{R_f^2}{(R_f+R_g)^2}\right)=4kTR_g\left(\frac{R_f^2}{(R_f+R_g)^2}\right)\)
• Una forma alternativa se muestra en la figura 7. Cada uno de los 5 pasos se explica de la siguiente manera:

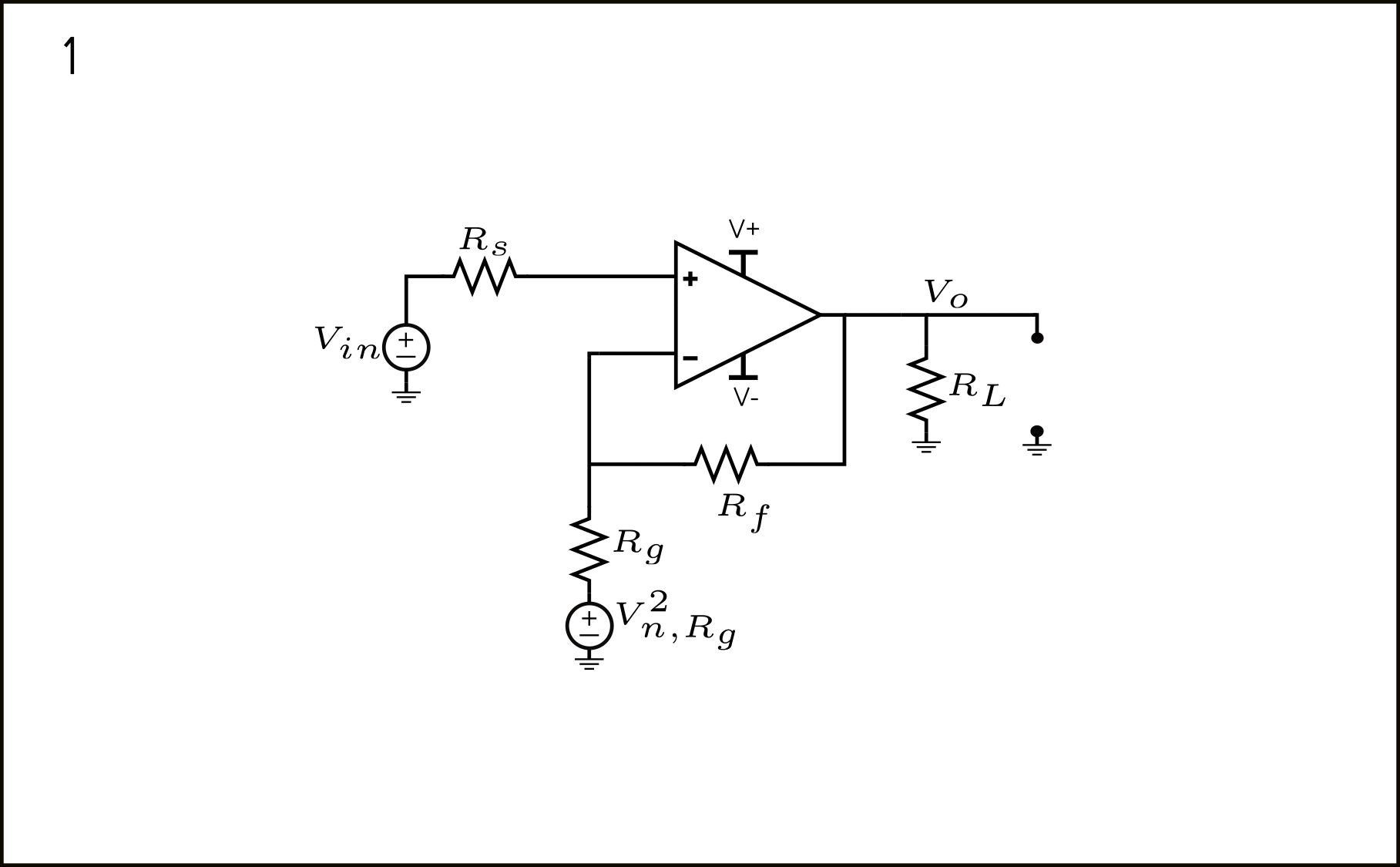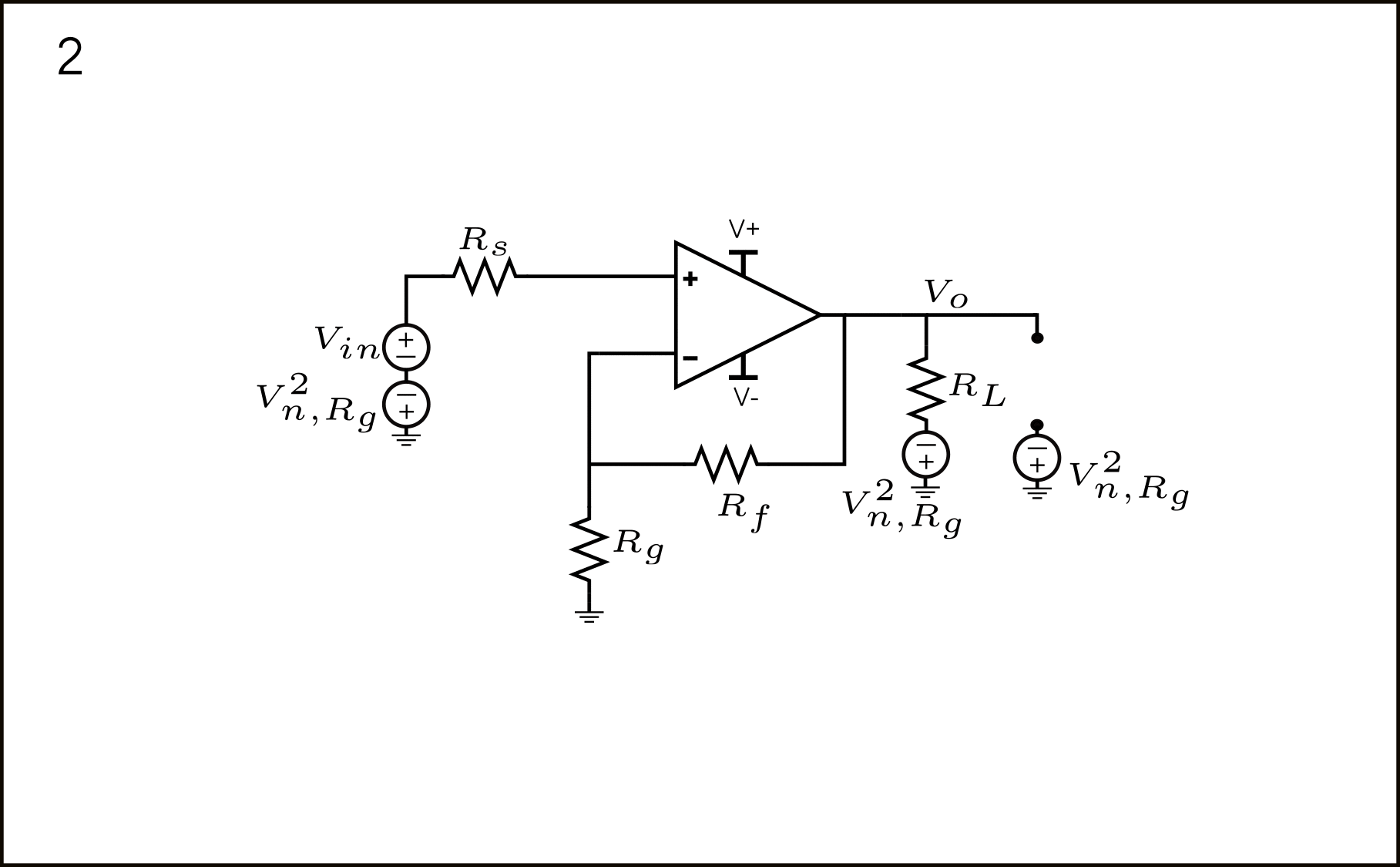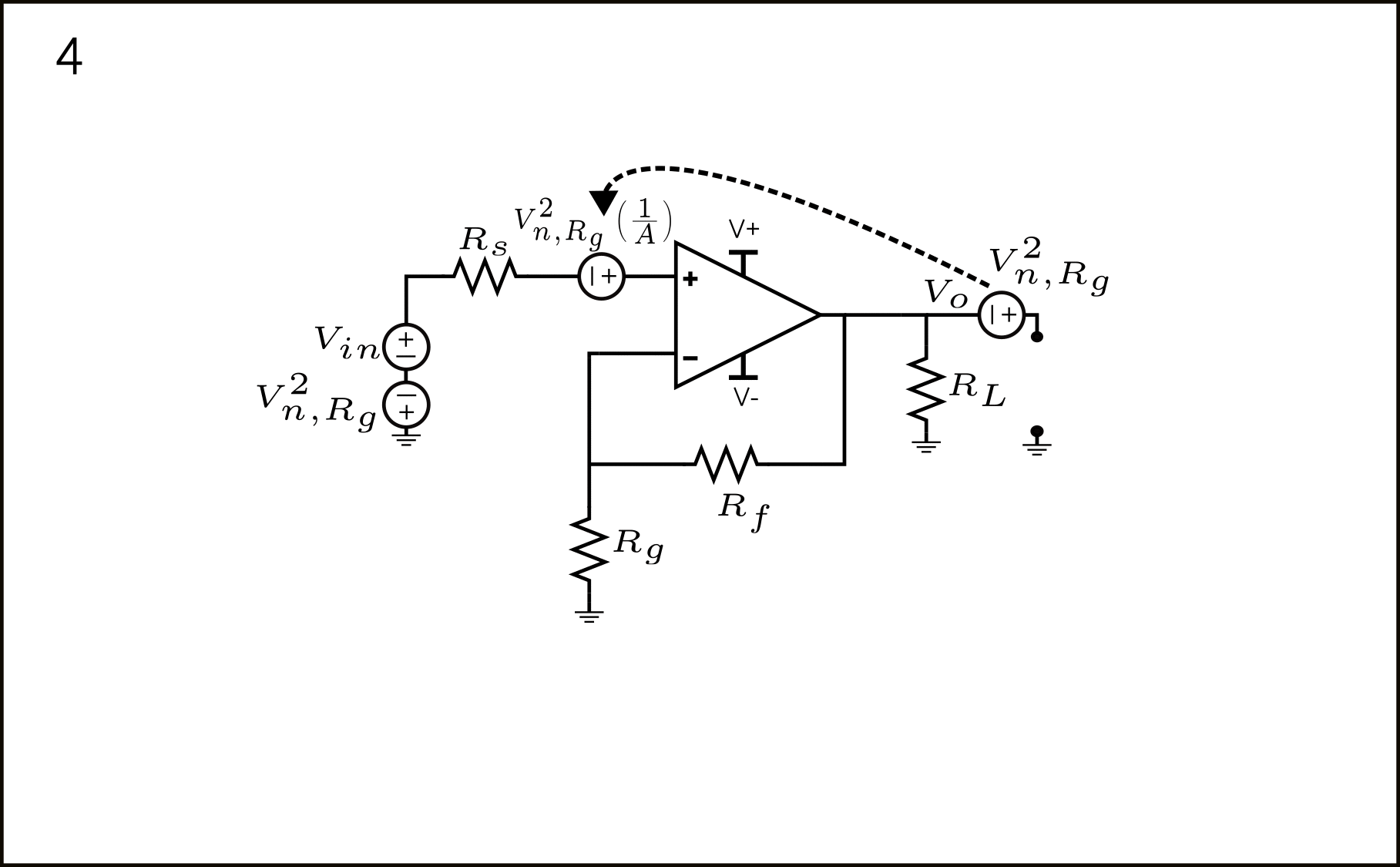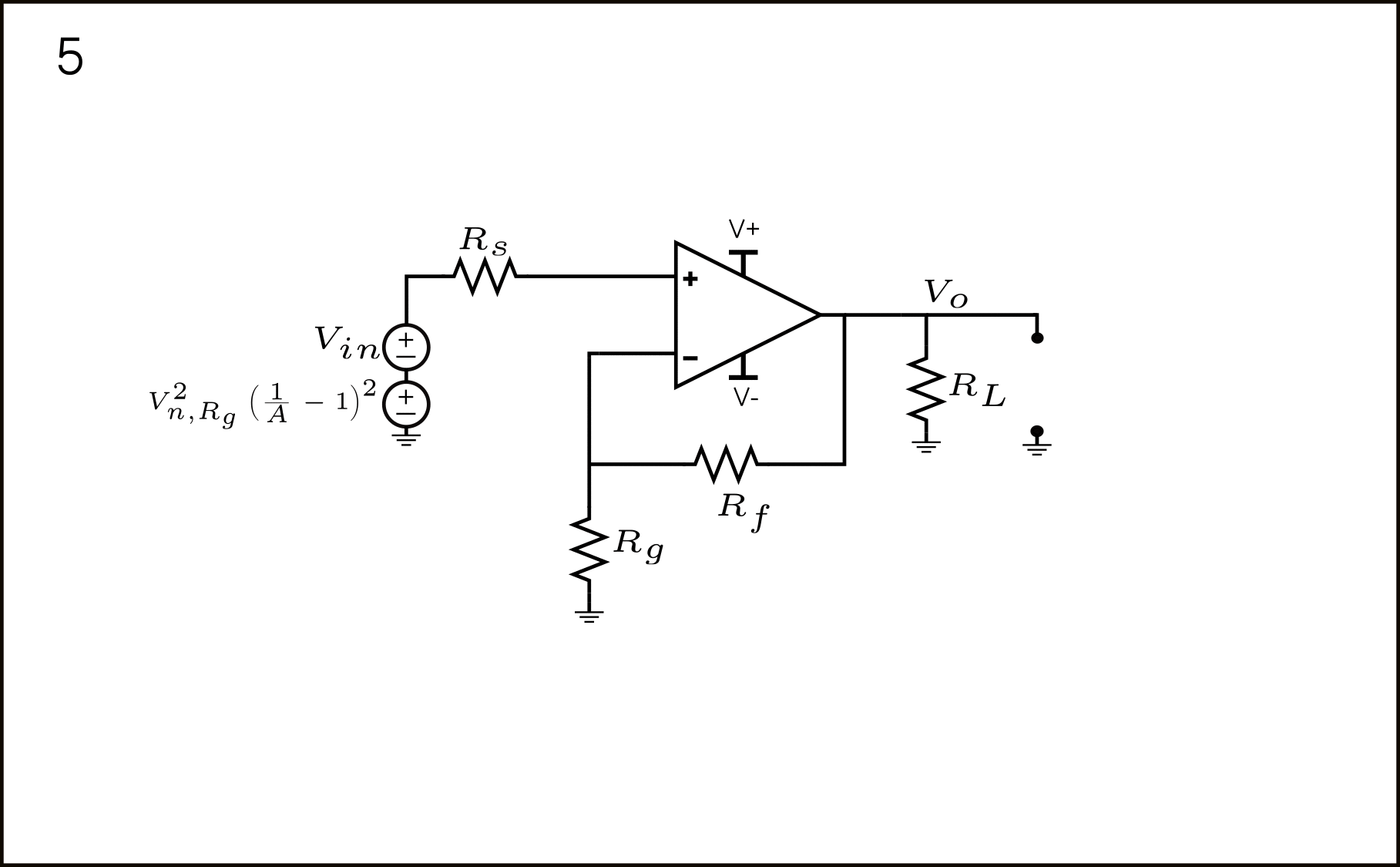
1. Esquema del amplificador con la fuente \(V_{n,R_g}^2\) modelada en serie con \(R_g\)
2. \(V_{n,R_g}^2\) se desplaza sobre el nodo de tierra, apareciendo en 3 nuevos lugares: en serie con la fuente de entrada \(V_{in}\), la carga \(R_L\) y la referencia de tierra del nodo de salida \(V_{o}\). Tenga en cuenta que todas las 3 nuevas fuentes resultantes están completamente correlacionadas. Volveremos a esto más tarde.
3. La \(V_{n,R_g}^2\) en serie con \(V_{in}\) ya está referida a la entrada. Nada que hacer al respecto, solo considere que tiene un signo negativo en comparación con la fuente de entrada. La otra fuente en serie con \(R_L\) puede ser ignorada de la misma manera que \(V_{n,R_L}^2\) podría ser ignorada. La última fuente que aparece en la referencia de tierra del nodo de salida \(V_{o}\) puede ser desplazada a través del abierto para, finalmente, aparecer en \(V_{o}\).
4. La fuente \(V_{n,R_g}^2\) que aparece directamente en \(V_{o}\) puede ser referida a la entrada por \(\frac{1}{A}\).
5. Finalmente, tenemos las contribuciones de \(V_{n,R_g}^2\) en serie en la entrada. Como se mencionó en el punto 3, sus contribuciones están completamente correlacionadas; por lo tanto, las sumamos como \(V_{n,R_g}^2(\frac{1}{A}-1)^2\) (teniendo en cuenta los signos).

Simplificando la última expresión obtenida en el punto 5: \(V_{n,R_g}^2(\frac{1}{A}-1)^2\), obtenemos:

\(V_{n,R_g}^2(\frac{1}{A}-1)^2=4kTR_g\left(\frac{R_g}{R_g+R_f}-1\right)^2=4kTR_g\left(\frac{R_f^2}{(R_g+R_f)^2}\right)\)

Que es exactamente lo mismo que la manera común de referirlo a la entrada, como debería ser.

\(V_{n,R_f}\) – Ruido de Voltaje asociado con la resistencia de realimentación \(R_f\)

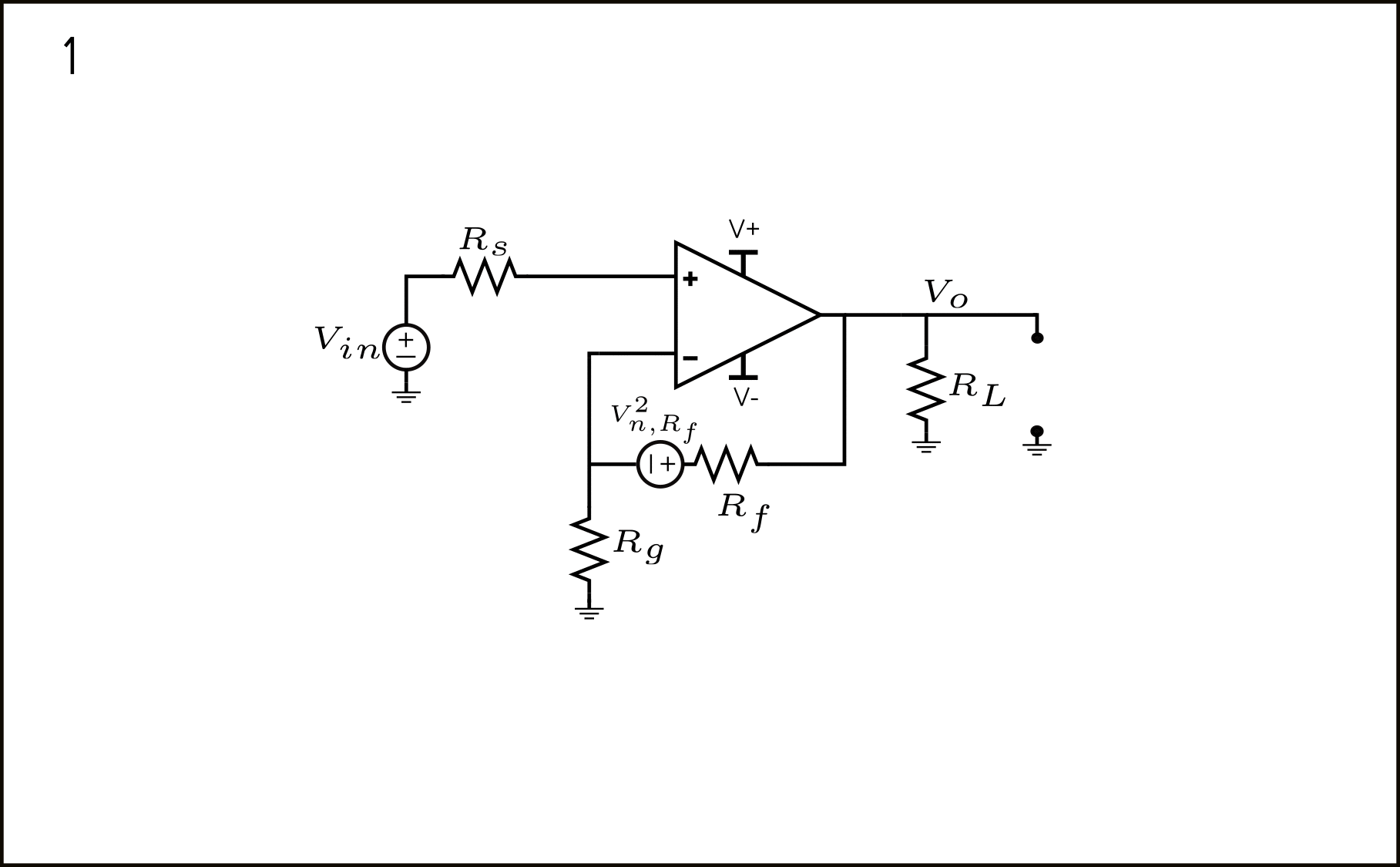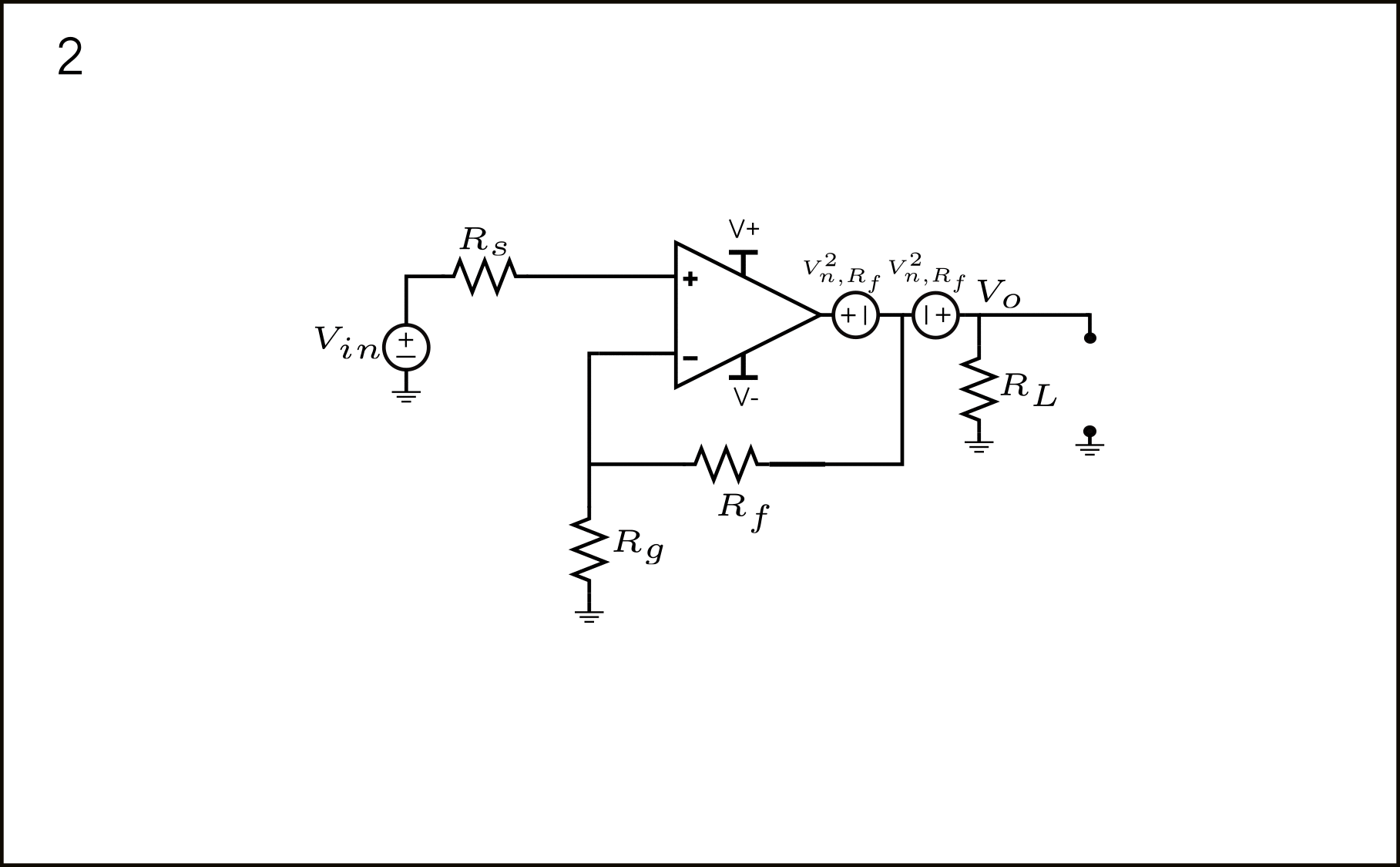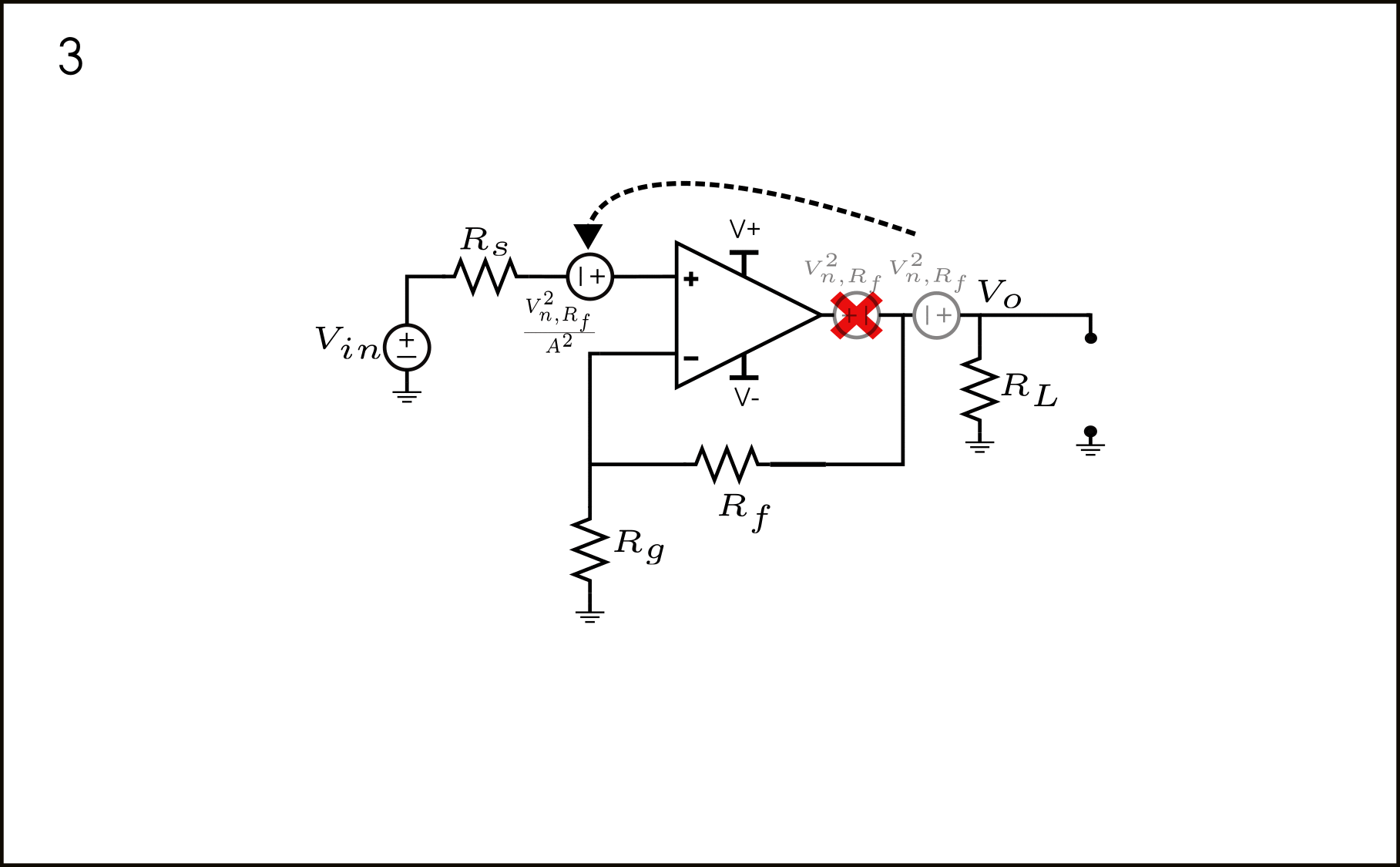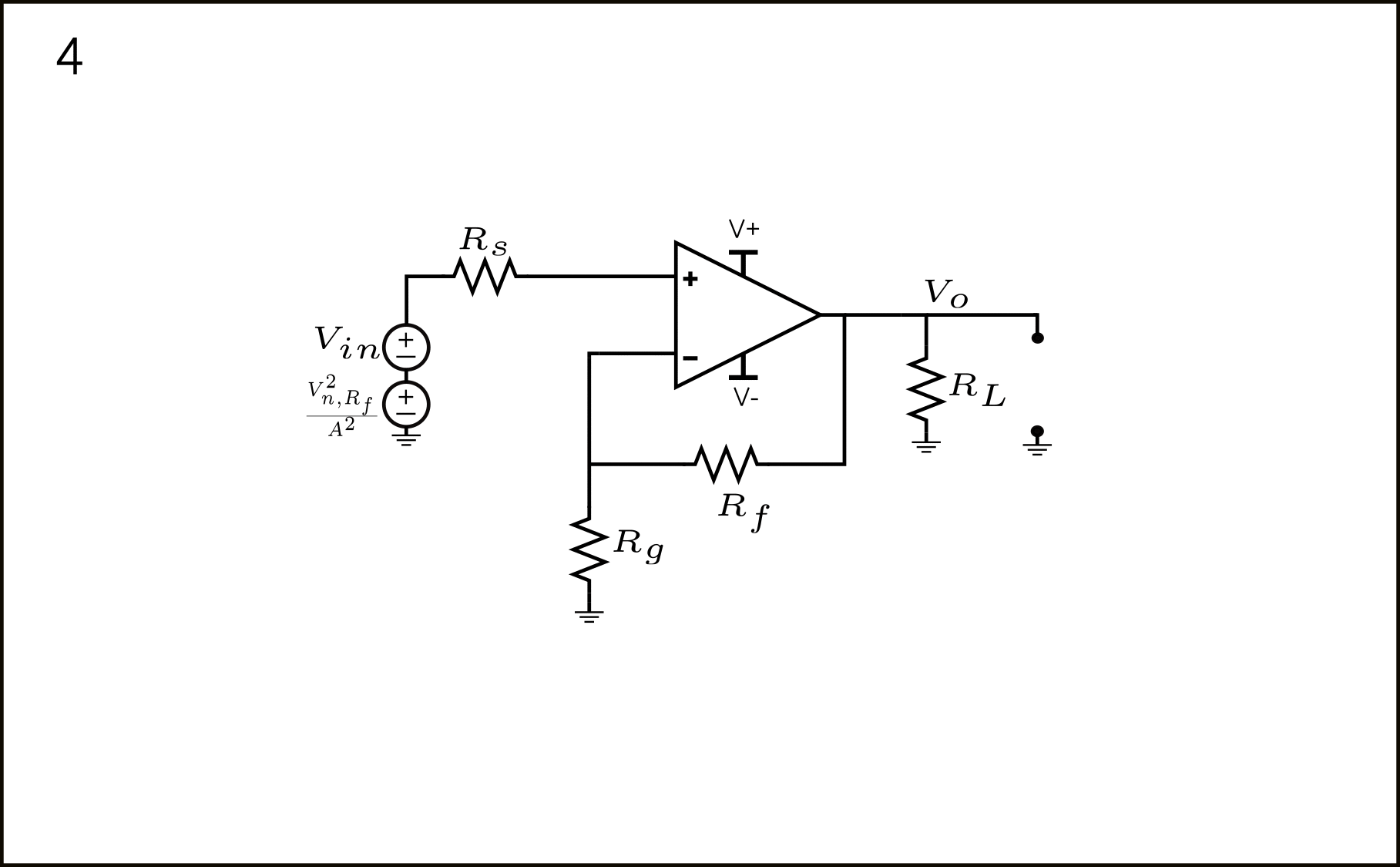
La fuente de ruido \(V_{n,R_f}^2\) está modelada en serie con \(R_f\), como se muestra en la figura 8.

Una conclusión rápida que podría surgir es que la fuente \(V_{n,R_f}^2\) podría ser desplazada a la salida, y así ser fácilmente referida a la entrada con \(\frac{1}{A}\). Aunque esto es correcto, hay una fuente de voltaje adicional que estamos olvidando.

De acuerdo con el teorema de desplazamiento de voltaje, cuando desplazamos una fuente de voltaje a través de un nodo, este voltaje debe aparecer en todas las demás ramas que conectan a un nodo. Este proceso de desplazamiento se muestra en los pasos 1 y 2 en la figura 9 a continuación.

Entonces, ¿qué pasa con esta fuente de \(V_{n,R_f}^2\) adicional directamente en serie con la salida del Op-Amp? En el paso 3 que se muestra arriba en la figura 9, dice que simplemente podemos despreciarla. ¿Por qué?

Esto se debe a que, como el op-amp es ideal, la ganancia de voltaje de este Op-Amp es infinita. Por lo tanto, cualquier fuente de voltaje directamente en la salida del Op-Amp debe ser referida a la entrada como 0 debido a la ganancia de voltaje infinita del Op-Amp.

Por lo tanto, esta fuente de ruido se refiere a la entrada como \(\frac{V_{n,R_f}^2}{A^2}=4kTR_f\frac{R_g^2}{(R_f+R_g)^2}\).

\(I_{n,OA}\) – Ruido de Corriente de Entrada del Op-Amp.

El ruido de corriente de entrada del Op-Amp puede ser modelado como se muestra en la figura 10.

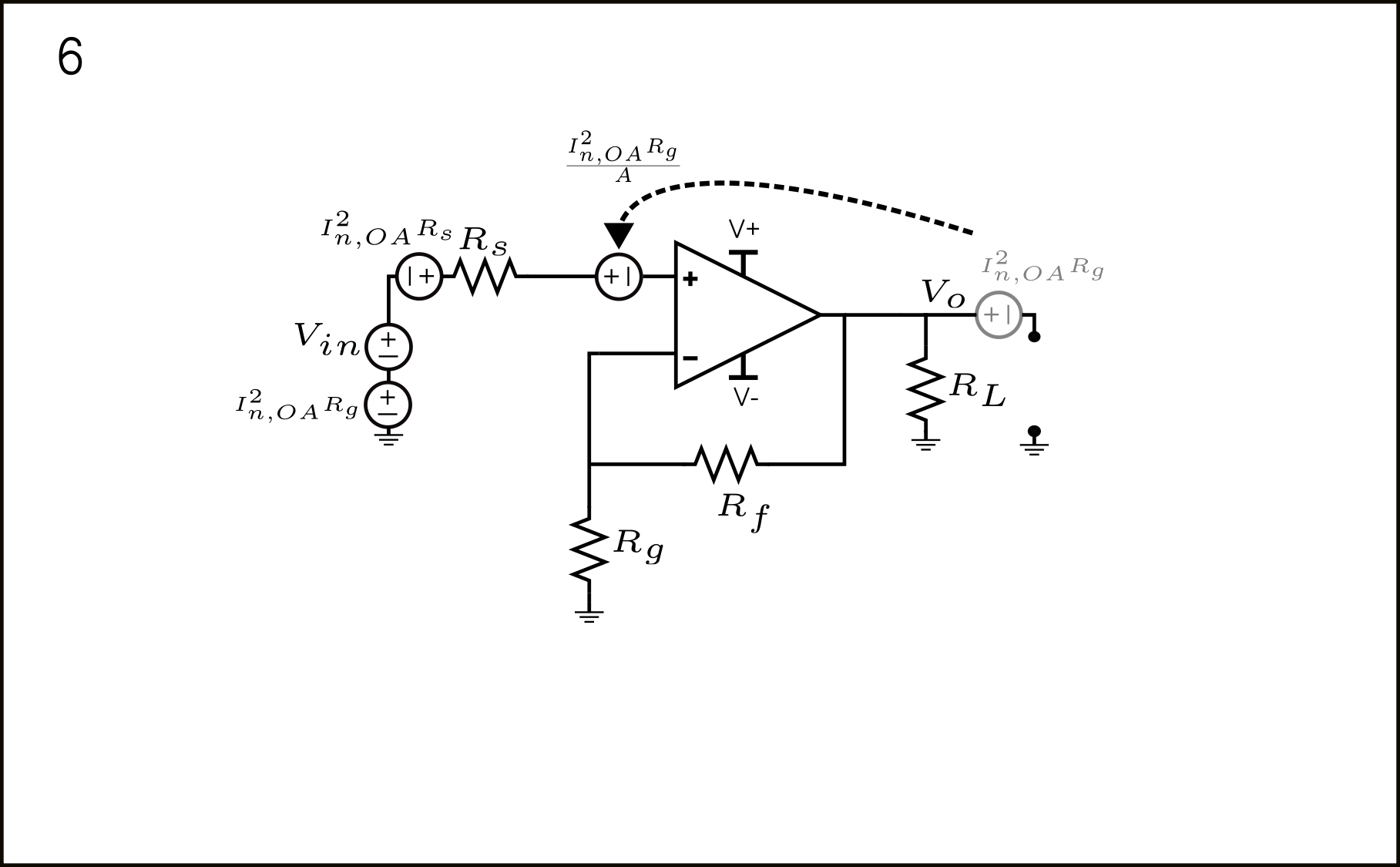
Probablemente este sea el más difícil de referir a la entrada, pero a través de los teoremas de desplazamiento de fuente de corriente y voltaje, el procedimiento se vuelve más manejable. Cada paso se muestra en la figura 11.

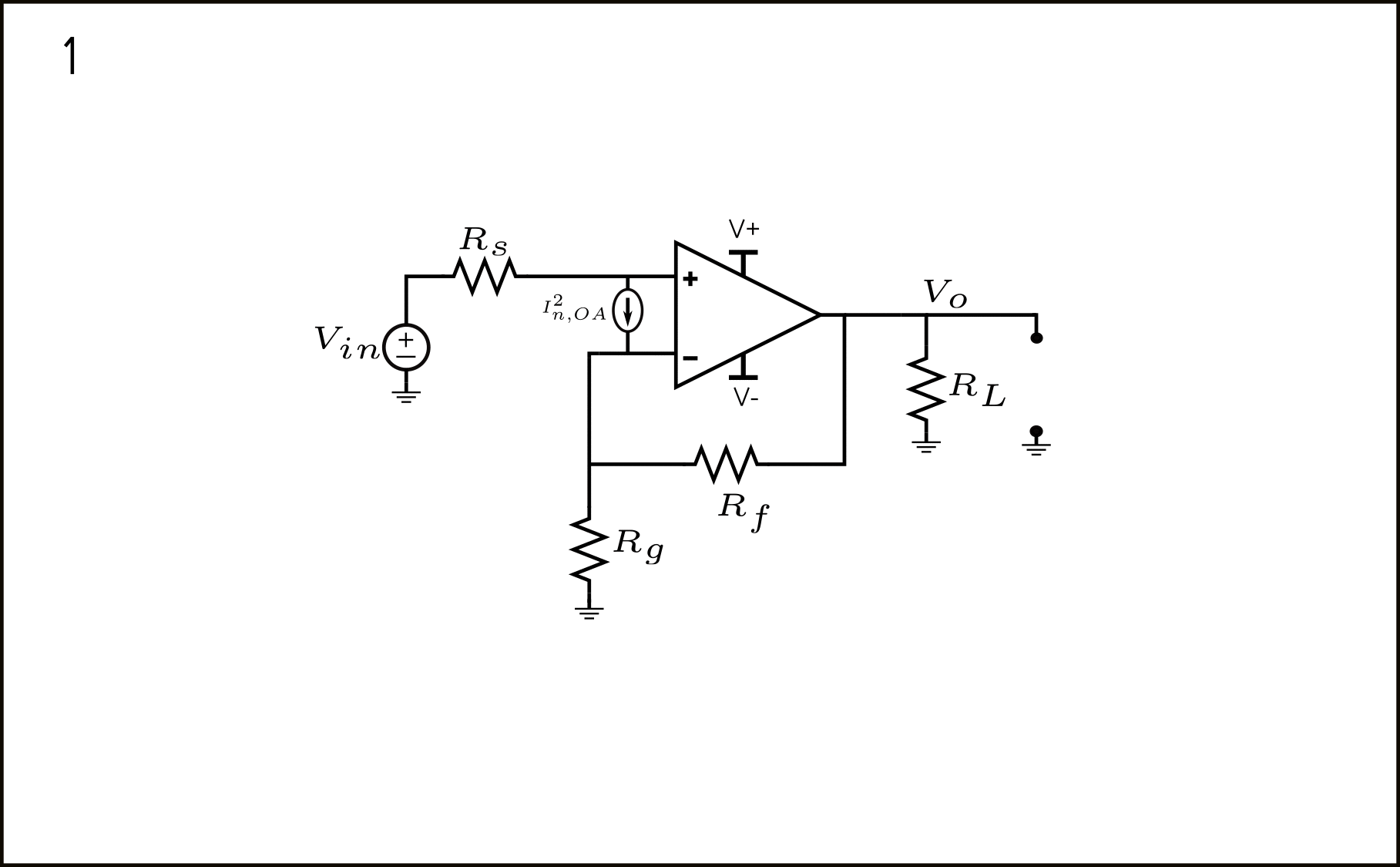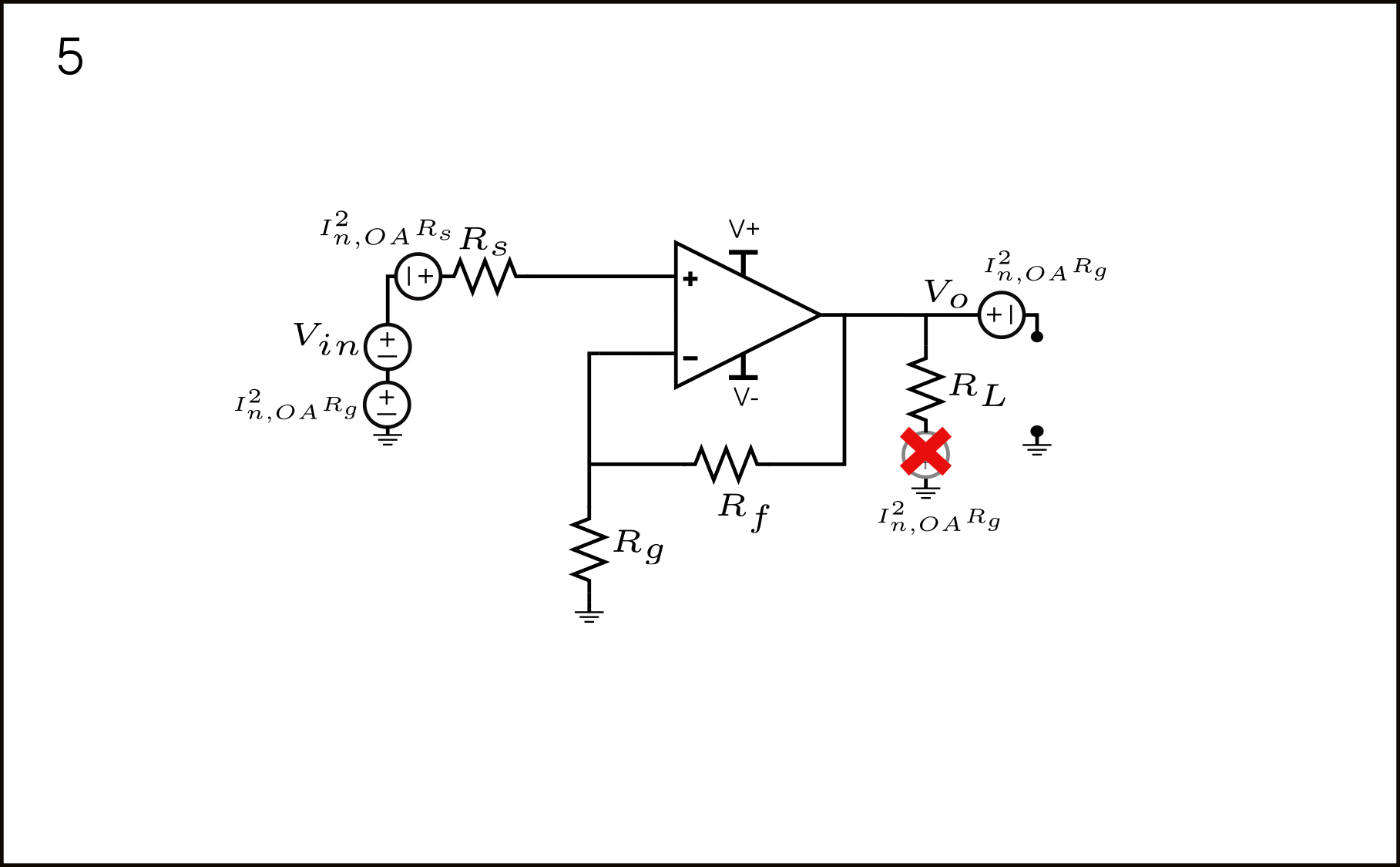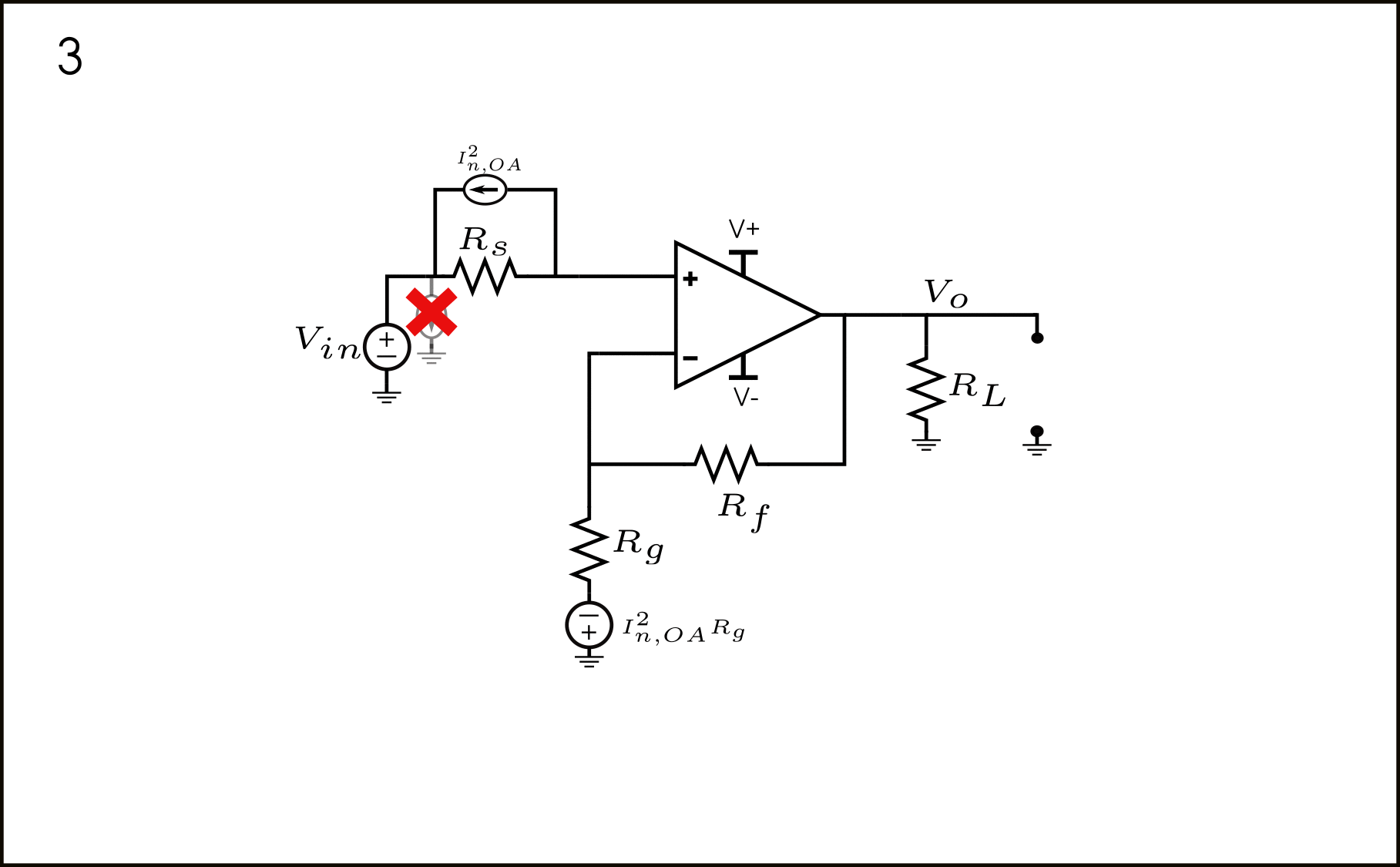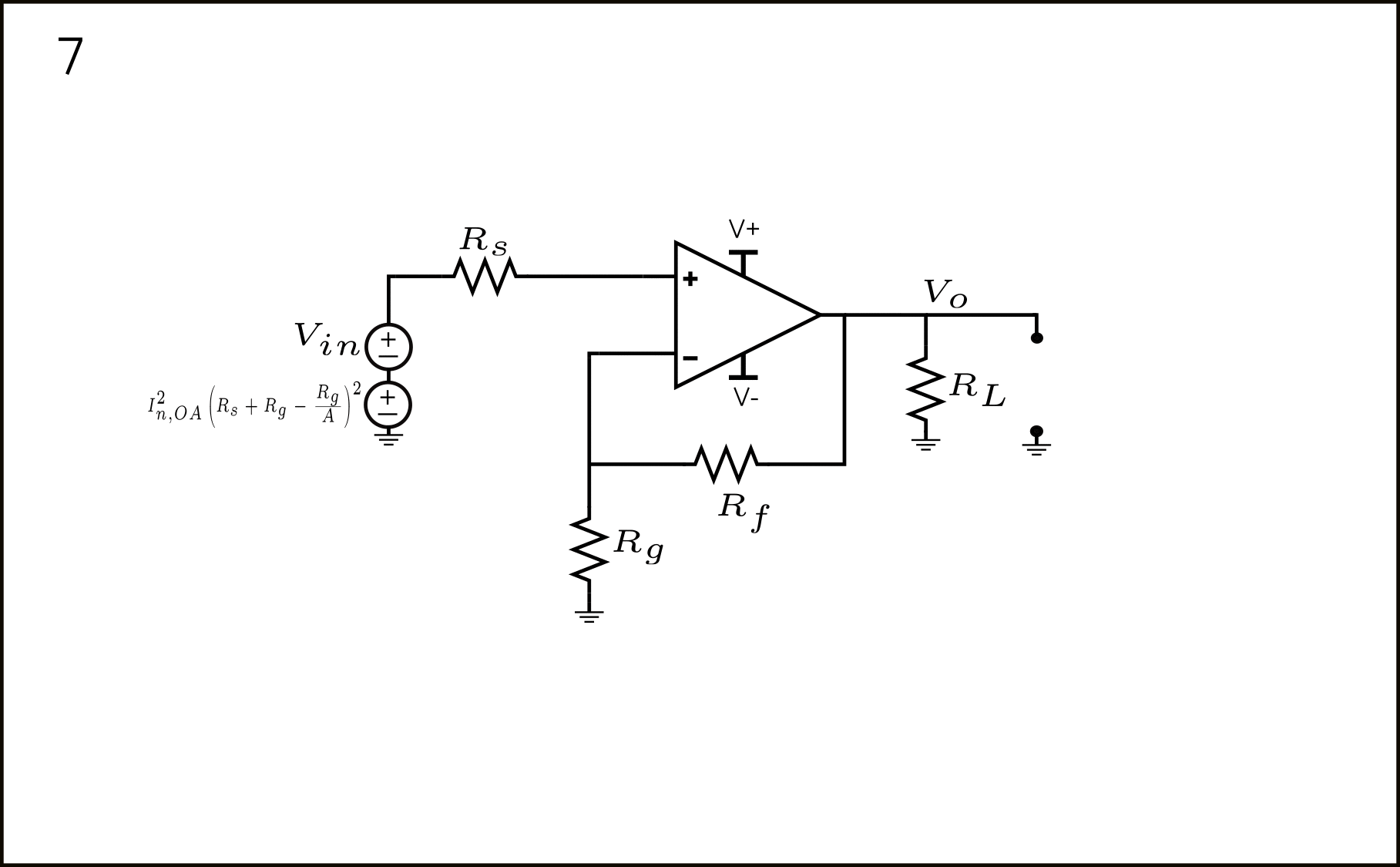
1. El Op-Amp mostrado con su ruido de corriente de entrada equivalente.
2. Usando el teorema de desplazamiento de fuente de corriente, obtenemos nuevas fuentes de corriente desde la entrada (+) del Op-Amp a tierra, y de tierra a la parte superior del resistor \(R_g\). Tenga en cuenta, nuevamente, que todas estas fuentes de corriente están correlacionadas. Volveremos a esto más tarde.
3. La fuente desde la entrada (+) del Op-Amp a tierra puede desplazarse, apareciendo así a través de \(R_s\) y \(V_{in}\). La fuente de corriente a través de \(V_{in}\) simplemente desaparece, ya que solo \(V_{in}\) puede definir un voltaje entre tierra y la entrada (+) del Op-Amp, y puede proporcionar cualquier corriente. Por otro lado, la corriente a través de \(R_s\) simplemente produce un voltaje \(I_{n,OA}^2R_s\). La fuente de corriente a través de \(R_g\) simplemente produce \(I_{n,OA}^2R_g\) ¹.
4. La fuente \(I_{n,OA}^2R_g\) puede desplazarse a través del nodo de tierra, apareciendo así en 3 lugares diferentes. La \(I_{n,OA}^2R_g\) en serie con \(V_{in}\) ya está referida a la entrada. Nada que hacer al respecto. La otra fuente está en serie con \(R_L\) La última fuente aparece en la referencia de tierra del nodo de salida \(V_{o}.\).
5. La fuente en la tierra del nodo \(V_{o}.\) puede desplazarse a través del abierto para, finalmente, aparecer en \(V_{o}\). La fuente en serie con \(R_L\) puede ser despreciada de la misma manera que \(V_{n,R_L}^2\) podría ser despreciada. La última fuente aparece en la referencia de tierra del nodo de salida \(V_{o}\) puede ser desplazada a través del abierto para aparecer directamente en serie con el nodo \(V_{o}.\).
6. La fuente \(I_{n,OA}^2R_g\) que aparece directamente en \(V_{o}\) puede ser referida a la entrada por \(\frac{1}{A}\).
7. Finalmente, sumando todas las fuentes de manera correlacionada, tenemos: \(I_{n,OA}^2\left(R_s + R_g – \frac{R_g}{A}\right)^2\).

Simplificando la expresión obtenida en el paso 7, llegamos a:

\(I_{n,OA}^2\left(R_s + R_g – \frac{R_g^2}{R_g+R_f}\right)^2=I_{n,OA}^2\left(R_s + \frac{R_gR_f}{R_g+R_f}\right)^2\)

Sumando todas las fuentes de ruido referidas a la entrada.

Para concluir sumamos las contribuciones de todas las fuentes de ruido referidas a la entrada:

\(V_{n,in}^2 = 4kTR_s + V_{n,OA}^2 + I_{n,OA}^2\left(R_s + \frac{R_gR_f}{R_g+R_f}\right)^2 + 4kTR_f\frac{R_g^2}{(R_f+R_g)^2} + 4kTR_g\left(\frac{R_f^2}{(R_g+R_f)^2}\right)\)

Simplificando aún más, llegamos a la expresión:

\(V_{n,in}^2 = 4kTR_s + V_{n,OA}^2 + I_{n,OA}^2\left(R_s + \frac{R_gR_f}{R_g+R_f}\right)^2 + 4kT\frac{R_fR_g}{R_f+R_g}\)

Finalmente, algunos comentarios son necesarios:

• El ruido referido a la entrada depende de la resistencia de fuente. Una alta resistencia de fuente puede llevar a un alto ruido referido a la entrada debido al ruido de corriente intrínseco del Op-Amp.
• La contribución de ruido por la red de realimentación puede ser modelada fácilmente por la combinación en paralelo de las resistencias de la red de realimentación, como \(4kT(R_g||R_f)\). Además, el ruido de corriente del Op-Amp también se refleja a través del producto de él y \(R_g||R_f\).
• Es obvio que una resistencia menor reducirá el ruido, pero lo hará a expensas del consumo de energía (en este caso, se deberá consumir más corriente por parte del Op-Amp para conducir la red de realimentación).
• Por ejemplo: la potencia requerida por el Op-Amp para conducir la red de realimentación (despreciando \(R_L\) y asumiendo \(R_{in}\) infinita del Op-Amp) se da por \(P_{out}=\frac{I_{out}^2}{R_f+R_g}\). Si hacemos una copia de todo este amplificador, y conectamos cada nodo copiado a su nodo original, y asumiendo que el ruido de corriente del Op-Amp es despreciable, la contribución de ruido de la red de realimentación se reducirá en 3dB mientras que el consumo de energía se duplicará (es decir, \(V_{n,\textrm{feedback network}}=\sqrt{4kT\frac{R_fR_g/4}{R_f/2+R_g/2}}=\sqrt{\frac{1}{2}}\sqrt{4kT\frac{R_fR_g}{R_f+R_g}}\) y \(\sqrt{\frac{1}{2}}=-3dB\)). Esta es una compensación fundamental entre ruido y potencia, por 2x la potencia, obtienes -3dB de reducción de ruido.

1. No estoy elevando al cuadrado las resistencias todavía para reflejar que deben sumarse de manera correlacionada al final \(I_{n,OA}^2(\dots + \dots)^2\).