Este artículo se inspiró en dos preguntas que leí en electronics.stackexchange.com sobre la polarización de la entrada (+) de un amplificador operacional con una resistor a tierra (\(R_b\) en la imagen a continuación).
Una de las preguntas era sobre porqué se necesita el resistor conectado a tierra y otra sobre la razón por la cual el ruido asociado al resistor puede ser ignorado a altas frequencias (ambas preguntas en inglés).

Aunque las respuestas ya están dadas en los vínculos de arriba (Yo también contribuí a las respuestas como ErnestoG), creo que son buenos ejemplos para introducir un teorema de circuitos no muy conocido que nos permite computar o calcular el ruido asociado con la resistencia \(R_b\). El teorema puede ser usado para otros escenarios en donde debamos calcular ruido, además de poder ser usado en derivar nuevas formas de polarizar un circuito (un tema mucho más avanzado. Será para otro artículo).
Este teorema es una consecuencia de la leyes de Kirchoff para voltaje y corriente. Nos permite mover las fuentes de voltage y corriente dentro del mismo esquemático y colocarlos en formas más explícitas para calcular el ruido. El teorema fue descubierto por T.H. Blakesley en 1894. Aquí hay un vínculo al artículo original (en inglés).
He encontrado vídeos interesantes en español discutiendo el teorema como este video. Sin embargo, en este artículo aplico el teorema a circuitos más prácticos que he encontrado en mi trabajo como diseñador de circuitos analógicos integrados.
El Teorema de Desplazamiento de Fuentes en Figuras
El teorema puede ser explicado con dos figuras, como se ven abajo.


Explicación – Versión de Fuentes de Corriente
Para explicar la versión de las fuentes de corriente de la figura 1, podemos escribir las ecuaciones de Kirchoff de corriente para el nodo 1 de la siguiente forma (asumiendo que las corrientes entrantes son negativas, y las saliente positivas):
\(0 = I + \cdots\)De la misma manera, para el nodo 2:
\(0 = -I + \cdots\)Se puede ver que el nodo 2 no sabe de dónde viene la corriente, sólo que hay una corriente \(I\) entrando en él. De la misma forma, el nodo 1 tampoco sabe a dónde va la corriente, sólo que sale de él.
Por lo tanto, podemos escoger, arbitrariamente, el nodo 3 para redireccionar la corriente \(I\) saliendo del nodo 1, y, al mismo tiempo, mandar esa misma corriente desde el nodo 3 al nodo 2. Tenemos que hacer esto para compensar la entrada de la corriente \(I\) al nodo 3, ya que este nodo no tenía esa corriente fluyendo por él originalmente. Esto es equivalente a añadir los siguientes términos a la ecuación de corriente de Kirchhoff para el nodo 3:
\(0 = -I + I \cdots\)Explicación – Versión de Fuentes de Voltaje
La versión de voltaje simplemente refleja que, si uno escribe la ecuación de voltage de Kirchhoff para mallas, un voltaje \(V\) existe en ella, sin importar en qué parte de la malla se encuentre.
Una forma más intuitiva de entender esto es imaginarnos colocando un medidor de voltaje en el extremo derecho de cada rama B, C y D en la figura 2 (suponga que \(V\) está conectado a tierra en su lado negativo). Obviamente, deberíamos medir un voltaje \(V\) en cualquiera de los extremos de esas ramas B, C y D. Por lo tanto, también podríamos suponer que la rama A está conectada a tierra y que las ramas B, C y D tienen un voltaje \(V\) cada una.
Divisor de Voltaje Resistivo
Cualquier estudiante de primer año de ingeniería eléctrica sabe cómo calcular la transferencia de un divisor de voltaje. Sin embargo, calcular el ruido referido a la entrada es otra historia.
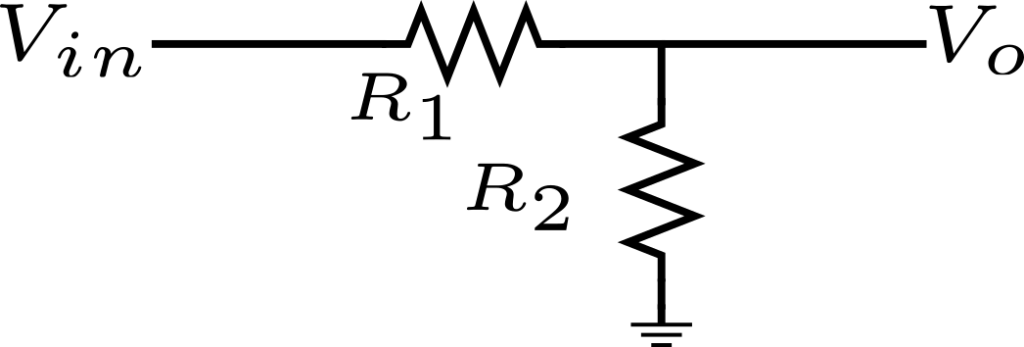
Queremos calcular la densidad de ruido referido a la entrada, es decir, el ruido equivalente del circuito en el nodo \(V_{in}\). Sabemos que la densidad espectral de la potencia del ruido térmico de cada resistor está dada por \(4kTR\), donde k es la constante de Boltzmann y T es la temperatura en Kelvin, mientras que R es el valor de la resistencia en ohmios \(\Omega\). Por lo tanto, el ruido referido a la entrada debe incluir la contribución total de ambos resistores.
Podemos reconocer, rápidamente, que la potencia de ruido de \(R_1\) referido a la entrada está dada por:
\(V_{n,R_1}^2=4kTR_1\)Esta es una parte de la contribución total de ruido. Sin embargo, obtener la contribución de \(R_2\) es un poco más complicado.
A continuación, se mostrarán 2 formas de calcular este ruido; una que es más familiar utilizando las funciones de transferencia del divisor de voltaje, y otra, más fácil, utilizando el teorema de desplazamiento de la fuente de corriente presentado anteriormente.
Cálculo de ruido de entrada – Uso de funciones de transferencia

El ruido de voltaje de \(R_2\) debe pasar por 2 funciones de transferencia antes de ser referido a la entrada.
Primero, hacia \(V_o\), el ruido se transfiere por \(\frac{R_1}{R_1+R_2}\) (es decir, la transferencia del divisor resistivo visto desde R2 como entrada). Luego, desde \(V_o\) a \(V_{in}\), se refiere por la inversa de la transferencia del divisor resistivo original, es decir, \(\frac{R_1+R_2}{R_2}\).
Por lo tanto, la contribución de ruido referida a la entrada de R2 es:
\(V_{n,in,R_2}^2 = 4kTR_2\left(\frac{R_1}{R_1+R_2}\right)^2\left(\frac{R_1+R_2}{R_2}\right)^2 = \frac{4kT}{R_2}R_1^2\)A partir de esta expresión, podemos reconocer que \(\frac{4kT}{R_2}\) es el ruido de corriente equivalente asociado con R2. El método que utiliza sólo el ruido de corriente de \(R_2\) en lugar de su voltaje se muestra en la sección siguiente.
Cálculo de Ruido de Entrada – Uso del Teorema de Desplazamiento de Fuentes de Corriente
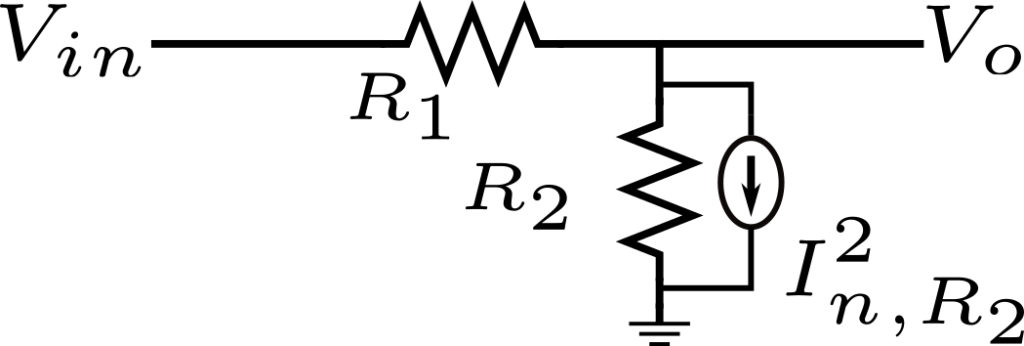
No hay una mejor explicación que la animación GIF a continuación para mostrar el procedimiento de referencia del ruido de corriente de \(R_2\) hacia la entrada como fuente de ruido de voltaje.
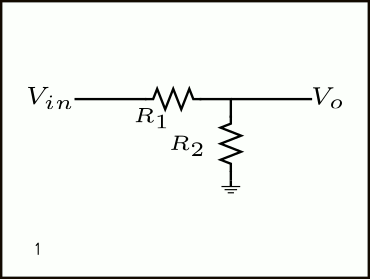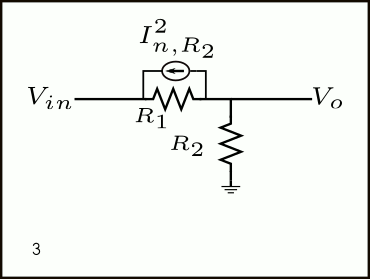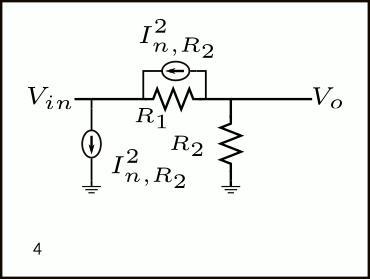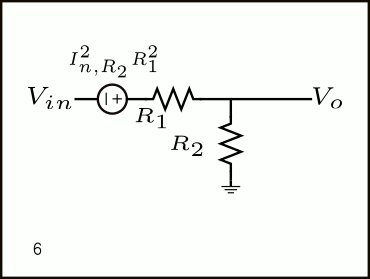
A continuación, la explicación de los pasos 1-6 de la Figura 6.
- Esquemático inicial
- Ruido de corriente de \(R_2\) es modelado como una fuente de corriente en paralelo a la resistencia
- El ruido de corriente de R2 se puede cambiar de lugar y colocar en paralelo con \(R_1\)
- Otra fuente de corriente debe agregarse desde \(V_{in}\) a tierra para cumplir con el teorema
- Esta última fuente se puede descartar ya que está en paralelo con la fuente de voltaje \(V_{in}\).
- Mientras tanto, el ruido de corriente de \(R_2\) en paralelo con \(R_1\) es multiplicado con dicha resistencia para obtener:
Por lo tanto, la densidad total de ruido referido a la entrada del divisor resistivo es:
\(V_{n,in,total}^2 = 4kTR_1 + \frac{4kT}{R_2}R_1^2\)Amplificador Operacional No Inversor – Ruido de Polarización de Entrada
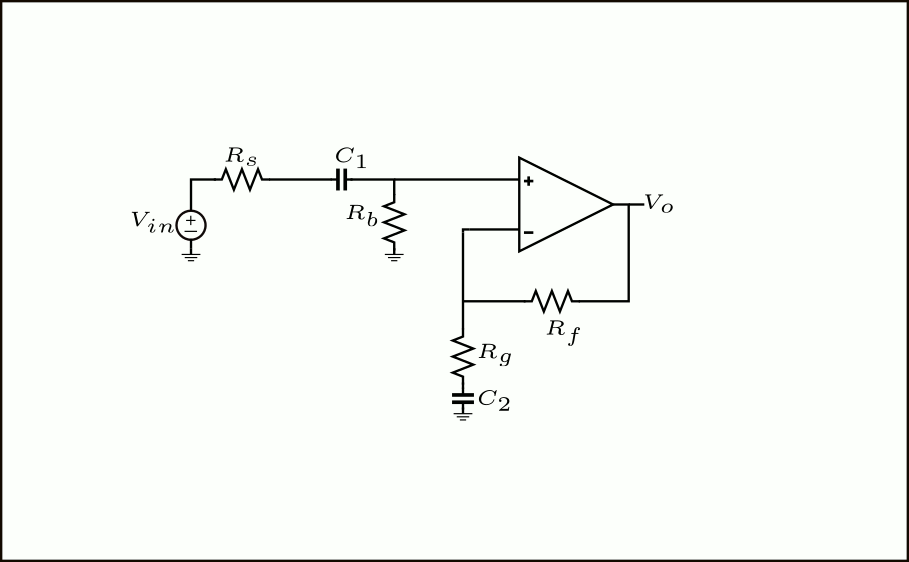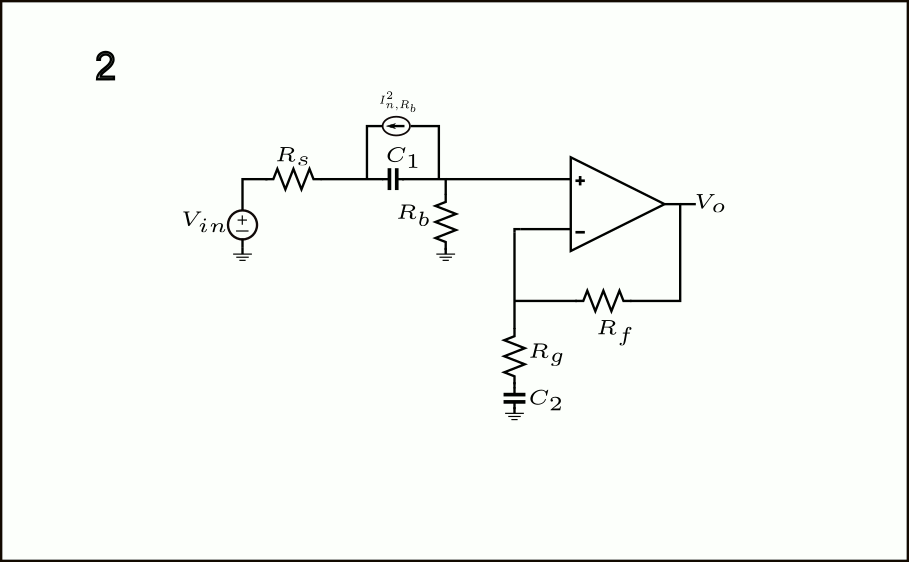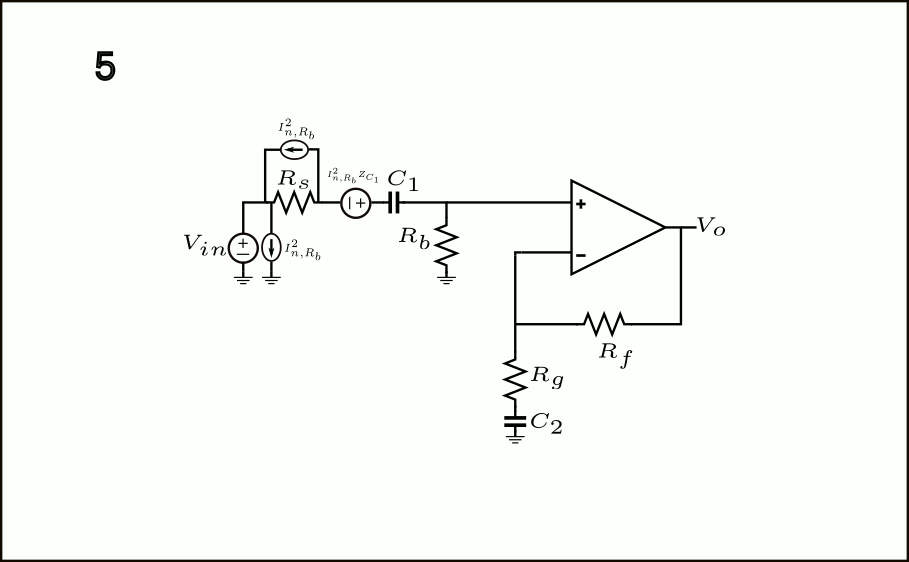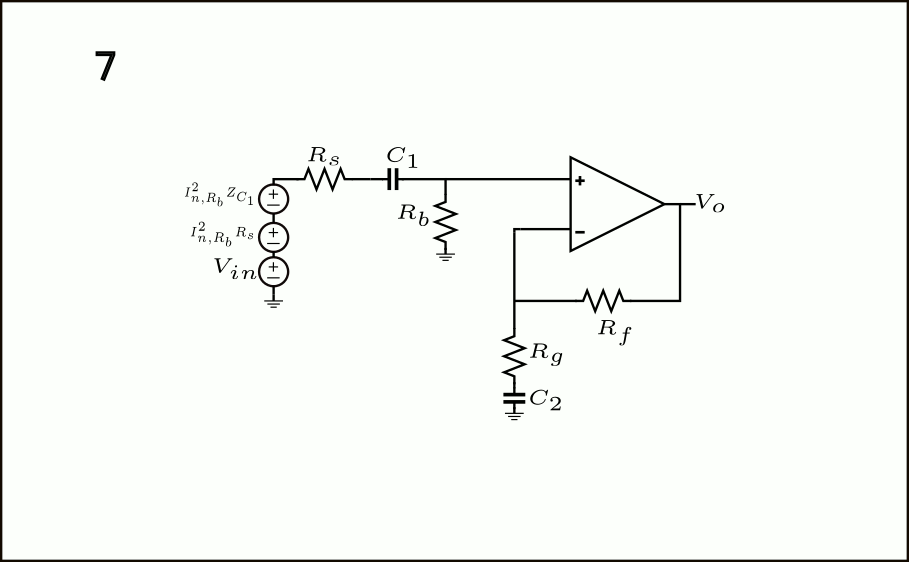
Una configuración típica de amplificador operacional no inversor se muestra a continuación.

\(R_s\) es la impedancia de la fuente de señal de entrada, mientras que \(C_1\) y \(R_b\) forman un filtro paso alto que aísla el amplificador de cualquier componente DC proveniente de la fuente. \(C_2\) se agrega de modo que, en DC, se convierta en un circuito abierto y el amplificador se convierta en un buffer de ganancia unitaria. Esto es necesario para evitar amplificar que la voltaje de desviación del amplificador operacional no sea amplificado hacia la salida por un factor \(1+\frac{R_f}{R_g}\).
¿Por qué se necesita \(R_b\)? Este tipo de polarización solo es necesaria si estamos interesados en amplificar componentes no DC. Debido a esto, el único objetivo de \(R_b\) es:
Polarizar la entrada (+) del Op-Amp a 0V.
También hay un artículo de Analog Devices (en inglés) que explica por qué se necesita el resistor \(R_b\), entre otros problemas del amplificador. Sin embargo, solo dan un par de declaraciones vagas sobre el ruido que \(R_b\) contribuirá a la fuente de entrada.
Ahora, estamos interesados en la contribución de ruido de \(R_b\) referida a la entrada.
En la siguiente subsección, se realiza el cálculo detallado (pero sencillo) del ruido referido a la entrada de \(R_b\) en esta configuración utilizando el teorema de desplazamiento de fuentes de corriente.
Cálculo del ruido referido a la entrada de \(R_b\)
El ruido de corriente asociado con \(R_b\) está dado por \(I_{n,R_b}^2=\frac{4kT}{R_b}\) y se puede modelar como una fuente de corriente en paralelo con el resistor en sí mismo, como se muestra en la figura a continuación.

Las fuentes de corriente y otros pasos se ilustran en la animación GIF a continuación:
Los pasos 1-7 se describen a continuación:
- El componente de fuente de ruido de corriente \(I_{n,R_b}^2\) asociado con \(R_b\) se muestra en paralelo con él.
- El término \(I_{n,R_b}^2\) ahora aparece en paralelo con \(C_1\).
- Para cumplir con el teorema, también necesitamos incluir \(I_{n,R_b}^2\) desde el terminal izquierdo de \(C_1\) a tierra.
- El componente \(I_{n,R_b}^2\) en paralelo con \(C_1\) se puede multiplicar con dicho capacitor para calcular la fuente de ruido de voltaje equivalente \(I_{n,R_b}^2|Z_{C_1}| = \frac{4kT}{R_b}\left(\frac{1}{\omega^2 C_1^2}\right)\).
- El otro componente \(I_{n,R_b}^2\) puesto en el paso 3 se puede volver a desplazar para estar en paralelo con \(R_s\) y con otro componente desde el terminal izquierdo de \(R_s\) a tierra (efectivamente, en paralelo con \(V_{in}\)).
- El \(I_{n,R_b}^2\) desde el terminal izquierdo de \(R_s\) se puede eliminar porque está en paralelo con la fuente de voltaje de entrada ideal \(V_{in}\). El componente en paralelo con \(R_s\) se puede multiplicar por dicha resistencia para obtener una fuente de ruido de voltaje de entrada equivalente de \(I_{n,R_b}R_s^2=\frac{4kT}{R_b}R_s^2\), tal como lo hicimos en el paso 4 con el capacitor \(C_1\).
- El componente de fuente de ruido de voltaje \(I_{n,R_b}^2|Z_{C_1}|\) calculado en el paso 4. se puede desplazar simplemente hacia la entrada ya que está en serie con \(R_s\), no hay transferencia entre ellos. Por lo tanto, finalmente tenemos la contribución total de ruido referido a la entrada debido a \(R_b\), que está dada por: \(\frac{4kT}{R_b}\left(\frac{1}{\omega^2 C_1^2}+R_s^2\right)\).
Cálculo de ruido referido a la entrada de \(R_b\) – Verificación mediante simulación
Como una prueba de cordura, usaré LTspice para verificar el cálculo realizado en la sección anterior.
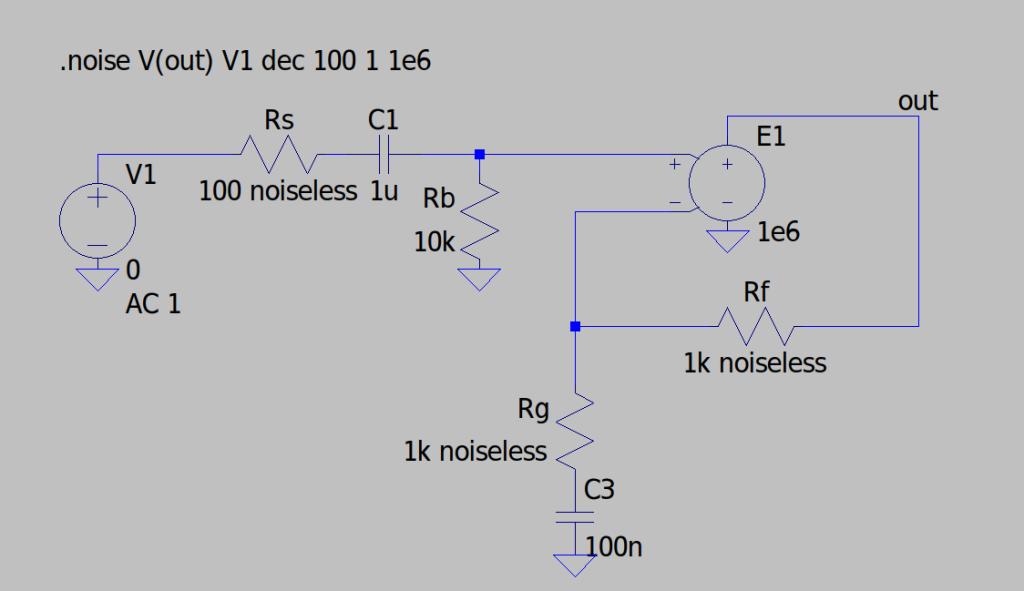
Para aislar la contribución de ruido de \(R_b\), utilizamos una fuente de voltaje controlada por voltaje con una ganancia de un millón, mientras que todas las resistencias (excepto \(R_b\)) están configuradas sin ruido. Para lograr eso, se necesita escribir «noiseless» luego del valor del resistor en LTspice, como se aprecia en la Figura 9. Esto hace posible que contribuyan al ruido referido a la entrada.
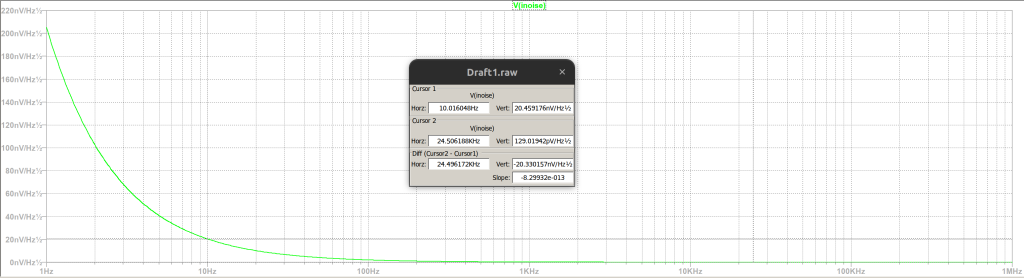
En la Figura 10, hemos medido el ruido en 2 frecuencias, como se muestra en la tabla a continuación:
| Frecuencia | Ruido Medido |
| 10 Hz | 20.45 \(nV/\sqrt{Hz}\) |
| 24.5 kHz | 129.01 \(pV/\sqrt{Hz}\) |
Como se derivó en la sección anterior, la tensión de ruido referida a la entrada se da por:
\(V_{in,n,R_b}=\sqrt{\frac{4kT}{R_b}\left(\frac{1}{\omega^2 C_1^2}+R_s^2\right)}\)
| Frecuencia | Ruido Medido | Ruido Calculado |
| 10 Hz | 20.46 \(nV/\sqrt{Hz}\) | 20.48 \(nV/\sqrt{Hz}\) |
| 24.5 kHz | 129.01 \(pV/\sqrt{Hz}\) | 128.9 \(pV/\sqrt{Hz}\) |
Los cálculos coinciden muy bien con las simulaciones. Los errores en el cálculo son realmente pequeños y se deben principalmente al redondeo de la frecuencia al decimal más cercano.
Con la expresión derivada anteriormente, podemos concluir que necesitamos hacer \(R_b\) lo más grande posible para reducir su contribución de ruido voltaje referida a la entrada.
Una pregunta que podría surgir es: pero, si hacemos \(R_b\) más grande, vamos a aumentar su ruido de voltaje, ¿cómo podemos entender, intuitivamente, que hacerlo más grande reducirá su contribución de ruido hacia la entrada?
Si imaginamos que hemos colocado una fuente de voltaje de ruido en serie con \(R_b\) a tierra, podemos notar que hay un divisor de voltaje entre \(R_b\) y \(R_s\) (asumir \(C_1\) como un cortocircuito para altas frecuencias). La función de transferencia se da por:
\(\frac{R_s}{R_s + R_b}\)Por lo tanto, cuanto más pequeño hacemos \(R_s\), o cuanto más grande hacemos \(R_b\), más pequeña será esta transferencia del ruido de voltaje de \(R_b\) hacia la entrada. Esto también destaca la importancia de saber que la impedancia de la fuente de señal es pequeña para nuestras frecuencias. De lo contrario, tendríamos un problema significativo de ruido.
Ejercicios
Amplificador con Realimentación Capacitiva
Cualquier amplificador operacional con realimentación capacitiva requiere que sus nodos de entrada y salida estén bien definidos en corriente continua (DC). Si el amplificador es independiente (es decir, no forma parte del camino de realimentación de otro amplificador cuyos puntos de operación DC ya están bien definidos), entonces se necesita una resistencia \(R_f\) en paralelo con el capacitor de realimentación, como se muestra en la figura 11.

Deriva la expresión de ruido referido a la entrada debido a \(R_f\), \(V_{n,R_f}^2\). Si queremos minimizar \(V_{n,R_f}^2\), ¿es mejor aumentar o disminuir el valor de \(R_f\)? ¡La respuesta podría sorprenderte!
Pistas/Sugerencias: Modela el ruido asociado con \(R_f\) como una fuente de corriente en paralelo y aplica el teorema del desplazamiento de la fuente de corriente. Puedes asumir que la fuente de tensión \(V_{in}\) es un corto circuito.
¿Algún comentario o sugerencia? Por favor, escríbanos abajo!

