Mientras que el símbolo de op-amp de 3 terminales es el elemento activo más utilizado en los libros de texto para analizar circuitos con retroalimentación, es limitante en el sentido de que no se puede aplicar retroalimentación en serie en la salida. Aunque la mayoría de los libros de texto utilizan un transistor (sugiriendo ya una implementación en particular) para implementar el cuarto terminal, es más elegante y útil abstraer todo el amplificador antes de sugerir una implementación en particular para este.

Un elemento activo universal que puede acomodar retroalimentación en serie en la salida (así como todos los otros tipos de retroalimentación utilizados alrededor de un símbolo de op-amp de 3 terminales) es el nullor.
El nullor fue denominado así por primera vez por H. Carlin y D. Youla en 1961.
Definición del Nullor
El nullor es una útil abstracción de un elemento activo de 4 terminales que está formado por un nullator y un norator, que hacen al nullor adecuado para el análisis de circuitos. Pueden ser considerados bloques de circuito ideales que proporcionan restricciones al nullor. No están realmente abstrayendo una implementación de circuito real individualmente. Además, solo tienen sentido cuando se utilizan como un par. Los circuitos teóricos que utilizan un número desigual de nullators y norators son posibles pero no realizables.

Las ecuaciones en la Figura 2 describen la funcionalidad del nullor. \(I_1=0\) y \(V_1=0\) podrían recordar a la mayoría de los lectores las reglas de oro del op-amp, a saber:
- No hay corriente fluyendo hacia los terminales de entrada del op-amp
- Ambas terminales de entrada están al mismo potencial. O, su diferencia es igual a 0 voltios.
Estas restricciones son establecidas por el nullator.
La tercera ecuación, impuesto por el norator, hace que las corrientes \(I_3\) y \(I_4\) sean las mismas (con el signo opuesto); en otras palabras, que la corriente entrante es igual a la saliente, mientras que la tensión de voltaje a través del norator es arbitraria.
Debe señalarse que, aunque parece que cumple con la función de un cortocircuito, no puede ser reemplazado por un cortocircuito. Un ejemplo posterior lo demostrará.
Si dibujáramos la \(I_3\) hacia atrás en la Figura 2, uno puede entender intuitivamente que la corriente que fluye a través del puerto superior derecho debe ser igual a la corriente que sale del puerto inferior derecho.
Si conectamos a tierra uno de los terminales, tendrá la funcionalidad exacta de un símbolo típico de op-amp:

Resolución de Circuitos con el Nullor
El nullor se puede utilizar en una variedad de abstracciones de circuito de alto nivel que pueden guiar la implementación del amplificador de retroalimentación:

Para mantener este artículo corto, solo se resolverá el amplificador de corriente a corriente, ya que es el circuito más inusual de las 4 topologías básicas. El circuito se resolverá de 2 maneras a continuación.

Resolución del Amplificador de Corriente a Corriente – Método I
Escribimos 2 expresiones de KCL para el nodo \(V_1\) y tierra virtual (0V).
\(\frac{V_1}{R_1}+\frac{V_1}{R_2}-I_L = 0\) \(I_{in} – \frac{V_1}{R_1} = 0\)Resolvemos para encontrar \(V_1\) en (2) y obtenemos \(V_1=I_{in}R_f\).
Reemplazamos \(V_1\) por la expresión obtenida en el paso 2 en la ecuación (1) y resolvemos para obtener \(\frac{I_L}{I_{in}}\).
Finalmente, derivamos:
\(\frac{I_L}{I_{in}} = 1+\frac{R_2}{R_1}\)¿No es el norator lo mismo que un cortocircuito?
Debemos anotar que, si, por error, asumimos que el norator es un simple cortocircuito, entonces, la primera expresión de KCL: \begin{align} \frac{V_1}{R_1}+\frac{V_1}{R_2}-I_L = 0 \end{align}
sería en realidad:
\begin{align} \frac{V_1}{R_1}+\frac{V_1}{R_2}+\frac{V_1}{R_L} = 0 \end{align}
Podríamos decir que \(V_1/R_L\) es \(I_L\). Y obtendríamos la misma expresión, pero con el signo opuesto. Sin embargo, esto tiene consecuencias problemáticas:
- A pesar de haber etiquetado \(V_1/R_L\) como \(I_L\), esto no cambia el hecho de que, ahora, \(I_L\) depende del valor de \(R_L\) mismo ya que hay división de corriente a través de 3 resistencias: \(R_1,R_2\) y \(R_L\).
- \(V_1\) ahora depende de \(R_L\)
Un amplificador de corriente debe proporcionar la corriente definida por su red de retroalimentación y no por su carga. Claramente, modelar el nullor de esta manera resulta en un amplificador de retroalimentación defectuoso.
Resolución del Amplificador de Corriente a Corriente – Método II
Una forma más sencilla de resolver esto es reconocer que \(I_L\) se divide en \(I_{in}\) y la corriente a través de \(R_1\). Por lo tanto, si quisiéramos encontrar la corriente que fluye a través de \(I_{in}\), podemos escribir: \begin{align} I_{in} = I_L\frac{R_1}{R_2+R_1} \end{align}
A partir de ahí, es sencillo resolver para \(\frac{I_L}{I_{in}}\).
Un Amplificador de Retroalimentación Más Complejo
En la Figura 4, podemos ver que el amplificador V-to-I (topología 4) tiene una transferencia negativa. Lo llamaremos un amplificador de transadmitancia a partir de ahora.
Como una digresión, uno podría ser capaz de reconocer que tal circuito puede ser implementado por el llamado amplificador de voltaje de emisor común.
La transferencia es la misma. Lo único que se debe agregar es que la corriente producida ahora se multiplica por la carga (en este caso, una predecible elegida por nosotros) para hacer un voltaje.

Sin embargo, ¿qué pasaría si quisiéramos realizar una transferencia de transadmitancia positiva?
Para lograr esto, podemos hacer uso de la poderosa abstracción del nullor para llegar a un concepto de transadmitancia no inversora.

El primer paso es reconocer que la dirección de \(I_L\) es positiva. Necesitamos implementar algo que tome una corriente de entrada, y la invierta a un voltaje del mismo signo que el voltaje de entrada.
Una forma de hacer esto es usar un amplificador de transimpedancia (amplificador de corriente a voltaje). Si la corriente en la entrada de este amplificador de transimpedancia está «saliendo» (o tiene un signo negativo), entonces el amplificador producirá un voltaje del signo opuesto, que será igual al voltaje de entrada. Por lo tanto, podemos llegar al siguiente esquema:

Resolver esto es bastante simple:
Por la Figura 8, podemos escribir la siguiente ecuación de KCL (asumiendo que todas las corrientes que fluyen fuera del nodo 0V son positivas):
\(\frac{0-V_{in}}{R_1} + I_L = 0\)Reorganiza para llegar a:
\(\frac{I_L}{V_{in}} = \frac{1}{R_1}\)Entonces hemos llegado a un amplificador de transadmitancia no inversora al abstraerlo con el nullor.
Verificación de Cordura
El amplificador ideal se implementa con VCVS ideal con una gran ganancia de voltaje para verificar el análisis. El esquemático a continuación muestra su implementación.
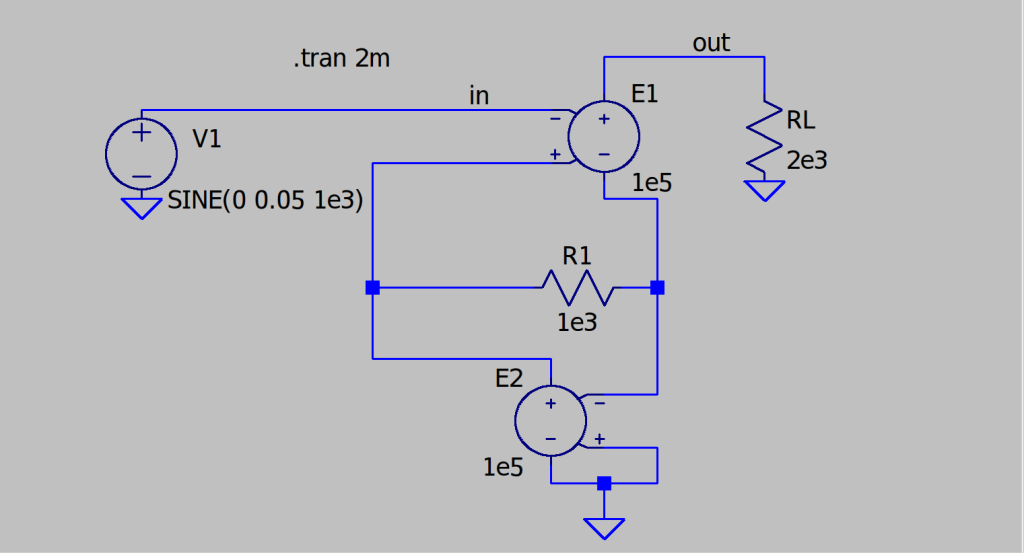
La simulación nos da una transadmitancia de 1.000 mS para \(R_1 = 1 k\Omega\).
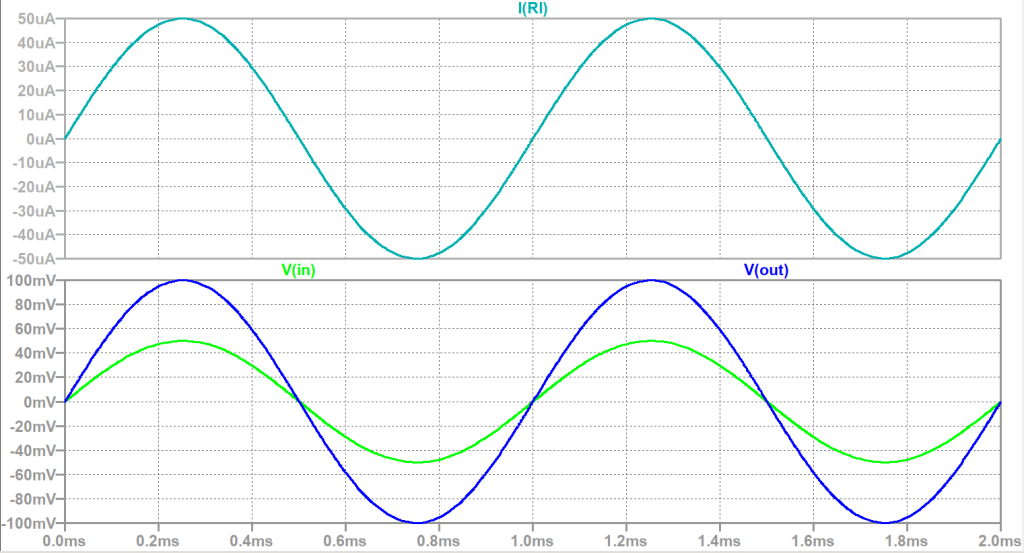
Conclusión
En este artículo, hemos explorado el nullor, una abstracción del circuito que ofrece una mayor flexibilidad y claridad para analizar y diseñar circuitos con retroalimentación. Hemos descubierto que la representación del nullor no está limitada a un símbolo particular de op-amp, sino que nos permite abordar una variedad de topologías de circuitos.
Nos hemos concentrado en la aplicación de esta abstracción a los amplificadores de corriente, destacando el análisis del amplificador de corriente a corriente y cómo abordar la cuestión de la retroalimentación en serie en la salida.
Finalmente, hemos mostrado cómo el nullor puede usarse para crear un amplificador de transadmitancia no inversor, un diseño que podría ser menos intuitivo utilizando solo los componentes de circuito convencionales.
References
¿Algún comentario o sugerencia? Por favor, escríbanos abajo!
